Números Hexadecimais
No capítulo sobre números binários, já há uma explicação genérica que explica um pouco melhor sobre sistemas númericos num geral e que já da uma noção de como o sistema hexadecimal funciona.
A palavra “hexa” simboliza o número 6, enquanto “deci” simboliza o número 10, de forma que hexadecimal simbolize um sistema númerico de 16 símbolos.
Os símbolos do sistema hexadecimal são : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D,E, F.
Podemos também pensar que A = 10, B = 11, C = 12, D = 13, E = 14 e F = 15 para facilitar o entedimento, levando em consideração uma provável familiaridade maior com números decimais.
O sistema númerico hexadecimal é extremamente útil pois ele tem um número de algarismos que é uma potência de dois, que efetivamente pode representar 4 digitos binários para cada digito hexadecimal, num mundo onde um byte é geralmente 8 bits, podemos representar um byte usando dois digitos hexadecimais ao invés de 8 digitos binários.
A vantagem do hexadecimal, é que ele pode ser efetivamente utilizado como uma representação mais compacta de números binários, é por isso que dificilmente veremos programadores utilizarem números binários, pois dificilmente há qualquer vantagem de binário sobre números hexadecimais.
Devido ao uso dos caracteres de A até F é comum utilizarmos um código similar a este para conversão um número representando um digito hexadecimal para caractere :
char hex_to_char(int hex)
{
hex = hex & 0xF; //Limita o número para 0 a 15
return (hex >= 10) ? (hex - 10 + 'A') : (hex + '0');
}
Conversão de binário para hexadecimal
A conversão de binário para hexadecimal é uma das mais fáceis, pois pode ser realizada de forma independente e paralela.
Cada 4 digitos de um número binário equivalem exatamente a um digito hexadecimal, a conversão de cada conjunto de 4 digitos pode ser feita em separado.
Isso é exemplificado na imagem abaixo, que como podem ver, leva a uma conversão extremamente simples :
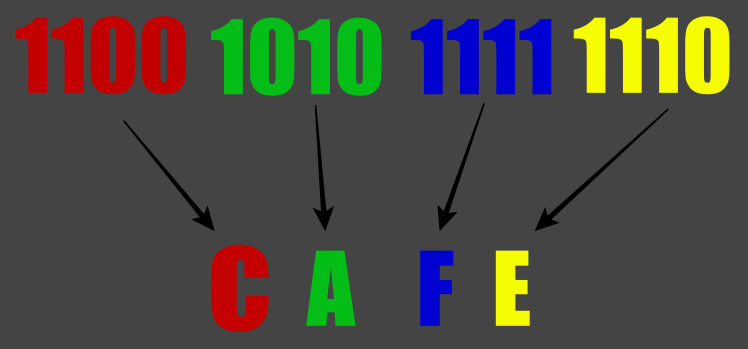
Onde o número 0b1100101011111110 vira 0xCAFE.
É comum essa conversão ser realizada mentalmente ao convertermos o número binário de 4 digitos para decimal e depois para hexadecimal.
0b1100é12em decimal, em hexadecimalC = 12, entãoC0b1010é10em decimal, em hexadecimalA = 10, entãoA0b1111é15em decimal, em hexadecimalF = 15, entãoF0b1110é14em decimal, em hexadecimalE = 14, entãoE
Conversão de hexadecimal para binário
A conversão de hexadecimal para binário é similar a conversão reversa, podemos converter cada digito hexadecimal em 4 digitos binários.
A conversão envolve converter cada digito individualmente e depois juntar todos, removendo os espaços.
Por exemplo para conversão de ABC para binário teremos :
Aé0b1010em binário (8+2=10(decimal) =A)Bé0b1011em binário (8+2+1=11(decimal) =B)Cé0b1100em binário (8+4=12(decimal) =C)
Logo o número resultante será a junção dos números 1010 1011 1100 (removendo os espaços), resultando em 0b101010111100.
Conversão de hexadecimal para decimal
Para convertermos um número em hexadecimal para decimal diretamente, podemos utilizar a notação posicional, seguindo as mesmas regras já explicadas no capítulo sobre números binários.
Por exemplo para convertermos 0xDC de hexadecimal para decimal :
//A = 10, B = 11, C = 12
//D = 13, E = 14, F = 15
13 * (16^1) //13*16 = 208
12 * (16^0) //12*1 = 12
//Logo, o resultado é
208+12 = 220
Teremos que 0xDC em hexadecimal é o número 220 em decimal.
Para conversão do número 0xFA8 em hexadecimal para decimal, teremos :
15 * (16^2) //15 * 256 = 3840
10 * (16^1) //10 * 16 = 160
8 * (16^0) //8 * 1 = 8
//Logo, o resultado é
3840+160+8 = 4008
Conversão de decimal para hexadecimal
Uma das formas é realizarmos a conversão para binário e depois convertermos de binário para hexadecimal.
Outra forma é utilizar o método da divisão, da mesma forma que utilizamos para binário.
No exemplo abaixo temos a conversão do número 3564 para hexadecimal :
3564 % 16 = 0xC (3564/16 = 222)
222 % 16 = 0xE (222/16 = 13)
13 % 16 = 0xD (13/16 = 0)
//Assim como no caso de números binários
//precisamos ler o resultado de baixo para cima
//Nesse caso ele resulta em :
0xDEC